Sainte-Laguë/Schepers
Der deutsche Physiker Hans Schepers, seinerzeit Leiter der Gruppe Datenverarbeitung des Deutschen Bundestages, schlug 1980 eine Modifikation des Sitzzuteilungsverfahrens nach d’Hondt vor, um die Benachteiligung kleinerer Parteien bei diesem Verfahren zu vermeiden. Das von Schepers vorgeschlagene Verfahren kommt mit einer anderen Berechnungsmethode zu identischen Ergebnissen wie das 1912 von dem französischen Mathematiker André Sainte-Laguë entwickelte Verfahren.
Das Verfahren nach Sainte-Laguë/Schepers wird bereits seit 1980 für die Sitzverteilung in den Ausschüssen und Gremien des Deutschen Bundestages eingesetzt. Seit 2009 ist das Verfahren auch für die Sitzzuteilung bei Bundestags- und Europawahlen maßgeblich. Bei Landtagswahlen findet es bereits seit 2003 in Bremen, seit 2008 in Hamburg, seit 2010 in Nordrhein-Westfalen, seit 2011 in Baden-Württemberg und Rheinland-Pfalz, seit 2012 in Schleswig-Holstein, seit 2022 in Bayern und seit 2023 in Sachsen Anwendung.
Bei diesem Verfahren, auch Divisormethode mit Standardrundung genannt, werden die jeweiligen Anzahlen der Zweitstimmen für die einzelnen Parteien durch einen gemeinsamen Divisor geteilt. Die sich ergebenden Quotienten werden standardmäßig zu Sitzzahlen gerundet, das heißt bei einem Bruchteilsrest von mehr oder weniger als 0,5 wird auf- oder abgerundet, bei einem Rest von genau gleich 0,5 entscheidet das Los. Der Divisor wird dabei so bestimmt, dass die Sitzzahlen in der Summe mit der Gesamtzahl der zu vergebenden Mandate übereinstimmen. Zur Berechnung gibt es drei verschiedene Methoden, die im Ergebnis rechnerisch gleich und damit rechtlich gleichwertig sind:
- Höchstzahlverfahren: Diese Methode folgt dem Gedanken des Verfahrens nach d’Hondt, wobei die jeweilige Stimmenanzahl durch 0,5, 1,5, 2,5 usw. geteilt und die Sitze wiederum fortlaufend nach absteigenden Höchstzahlen zugeteilt werden. Hintergrund ist, dass bei der Berechnung nach d’Hondt der volle Anspruch auf einen Sitz zugrunde gelegt wird und deshalb ganze Zahlen zur Teilung verwendet werden, wodurch aber kleinere Parteien unverhältnismäßig spät den ersten Zugriff und weitere erhalten. Demgegenüber sind hier die Zuteilungsvoraussetzungen für einen Sitz herabgesetzt, so dass der Zugriff bereits dann erfolgt, wenn die Voraussetzungen hierfür erst zur Hälfte erfüllt sind, wenn also Anspruch auf mehr als einen halben Sitz besteht.
- Rangmaßzahlverfahren: Hier werden statt der Höchstzahlen die Kehrwerte betrachtet und die Sitze fortlaufend nach diesen aufsteigenden Rangmaßzahlen beschrieben.
- Iteratives Verfahren: Nach dieser Methode wird im ersten Schritt eine Näherungszuteilung berechnet, indem die Gesamtanzahl aller zu berücksichtigenden Stimmen durch die Gesamtanzahl der zu verteilenden Sitze geteilt und auf diese Weise ein vorläufiger Zuteilungsdivisor ermittelt wird. Etwa verbleibende Diskrepanzen werden in den folgenden Schritten durch Herauf- oder Herabsetzung des Zuteilungsdivisors so lange abgebaut, bis die Endzuteilung erreicht ist, bei der die Sitzzuteilung mit der Anzahl der zu vergebenden Sitze übereinstimmt.
Der Gesetzgeber hat bei der Einführung des Verfahrens nach Sainte-Laguë/Schepers für die Sitzzuteilung bei den Wahlen zum Deutschen Bundestag das letztgenannte iterative Verfahren gewählt. Danach wird die Sitzzuteilung bei dem bereits oben verwendeten Rechenbeispiel wie folgt berechnet:
Verfahren nach § 6 Absatz 2 Bundeswahlgesetz (BWG) mit Zuteilungsdivisor
Formel:
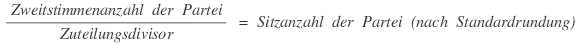
Ermittlung des Zuteilungsdivisors (Maßstab: Verteilung so vieler Sitze auf Landeslisten wie Sitze zu vergeben):
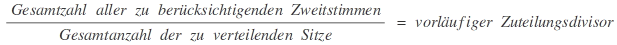
Gegebenenfalls Herauf- bzw. Herabsetzung des Zuteilungsdivisors, bis Berechnung in der Summe die Summe der zu verteilenden Sitze ergibt.
Gesamtzahl der Sitze abzüglich der Sitze erfolgreicher Einzelbewerber (Kreiswahlvorschläge gemäß § 20 Absatz 3 BWG) oder erfolgreicher Parteibewerber, wenn die Partei weniger als fünf Prozent der gültigen Zweitstimmen und weniger als drei Direktmandate errungen hat oder in dem betreffenden Land nicht mit einer Landesliste zugelassen ist (§ 6 Absatz 2 Satz 6 i. V. m. § 6 Absatz 1 Satz 3 BWG).
Beispiel: Zuteilung von 8 Sitzen
1. Schritt:
| Partei | Berechnung | Ergebnis nach Standardrundung = danach zuzuteilende Sitze |
|---|---|---|
| A |  |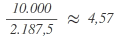
5 |
| B |  |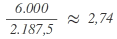
3 |
| C |  |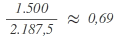
1 |
Da bei der Berechnung mit dem Zuteilungsdivisor 2.187,5 insgesamt 9 Sitze auf die Parteien entfallen, aber nur 8 Sitze zu vergeben sind, muss der Zuteilungsdivisor heraufgesetzt werden, bis die Berechnung der Sitzzuteilung in der Summe die Zahl der zu vergebenden Sitze ergibt. Hierfür wird nun die Berechnung mit dem erhöhten Zuteilungsdivisor von 2.300 erneut durchgeführt:
2. Schritt:
| Partei | Berechnung | Ergebnis nach Standardrundung = danach zuzuteilende Sitze |
|---|---|---|
| A |  |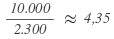
4 |
| B |  |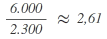
3 |
| C |  |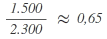
1 |
Das Verfahren nach Sainte-Laguë/Schepers beseitigt Paradoxien, die bei der Sitzzuteilung nach Hare/Niemeyer auftreten können.
Stand: 11. Juli 2024